Eugenio Bianchi
Associate Professor of Physics
The Pennsylvania State University
ebianchi@psu.edu
Institute for Gravitation and the Cosmos
315 Whitmore Lab
Ph.D. 2010 Scuola Normale Superiore
My work focuses on quantum gravity and quantum information. The objective of my research is to understand the quantum nature of spacetime geometry. To this end, I investigate diverse phenomena across loop quantum gravity, primordial cosmology, black holes, condensed matter physics, quantum chaos, and quantum thermalization. My research strategy is to cultivate cross-fertilization across subfield boundaries, contributing new insights and tools for exploring the quantum nature of spacetime.
inspirehep.net/authors/1032605
orcid.org/0000-0001-7847-9929
Loop Quantum Gravity and Spinfoams
At curvature lengths comparable to the Planck length, quantum effects become dominant and we need to go beyond Einstein's General Relativity to predict the dynamics of spacetime geometry. Loop Quantum Gravity provides a concrete mathematical framework for quantum geometry. Spinfoams describe its covariant dynamics. You can find an introduction to this mathematical framework and its phenomenological aspects in:
A short review of loop quantum gravity
Abhay Ashtekar and Eugenio Bianchi
2104.04394 [gr-qc] Rept. Prog. Phys. (2021)
Some highlights:
Bohr-Sommerfeld volume spectrum with H. Haggard (PRL 2011, PRD 2012)
Quantum Polyhedra with P. Dona and S. Speziale (PRD 2011, CQG 2011)
The Length Operator (NPB 2009)
LQG as a Topological Field Theory with Defects (GRG 2014)
Semiclassical Correlations with C. Rovelli, S. Speziale and L. Modesto (CQG 2006, NPB 2008)
Coherent States with E. Magliaro, C. Perini and Y. Ding (PRD 2010, NPB 2009, PRD 2010, PRD 2011)
Spinfoam Cosmology with C. Rovelli and F. Vidotto (PRD 2010)
Spinfoam Fermions with W. Wieland, M. Han, C. Rovelli, E. Magliaro and C. Perini (CQG 2013)
Squeezed Vacua with L. Hackl, J. Guglielmon and N. Yokomizo (PRD 2015, PRD 2016)
Bell-Networks with N. Yokomizo, B. Baytas, I. Vilensky and P. Dona (PRD 2018, PRD 2019)
Causal Structure with P. Martin-Dussaud (Universe 2024)
Hierarchy of Entanglement with E. Livine (Handbook 2023)
Gravitational Parity Violation with M. Rincon-Ramirez (2024)
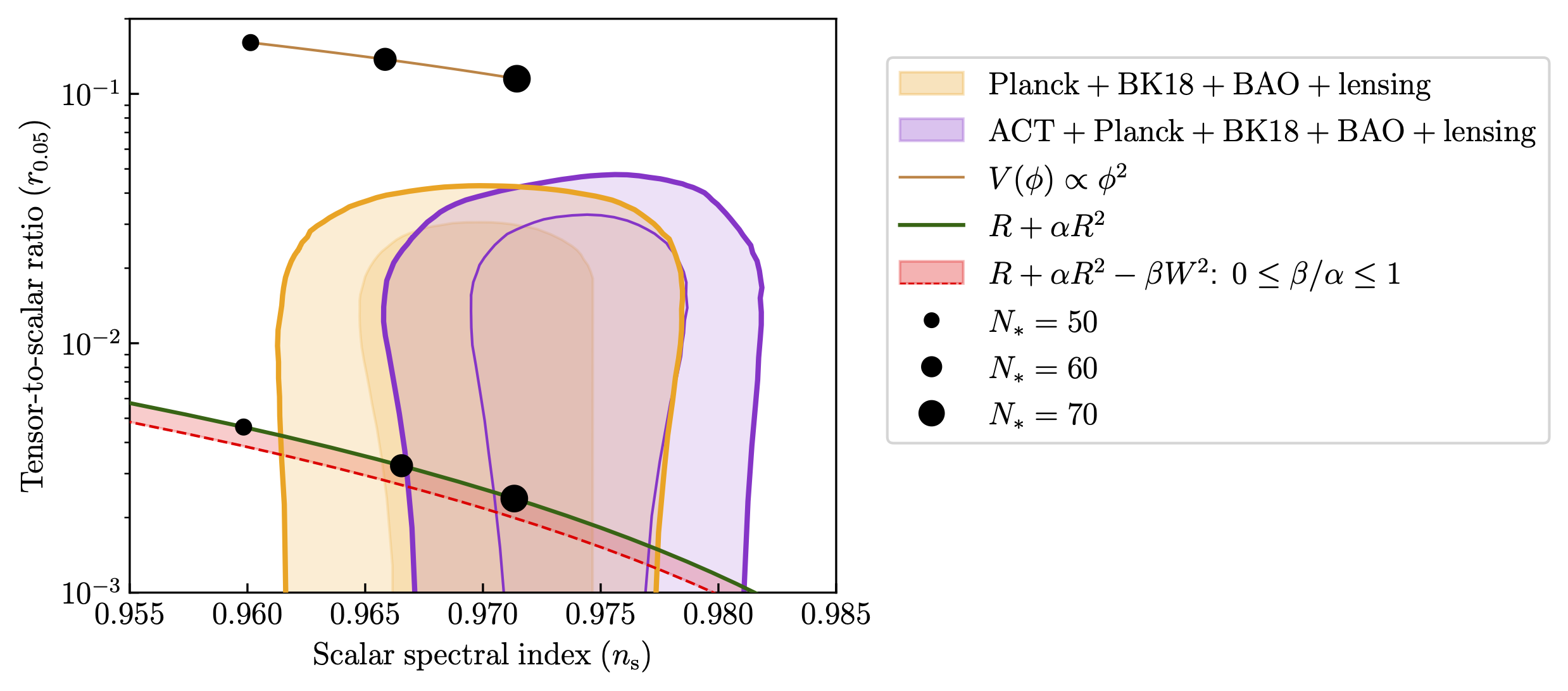
Primordial Cosmology
The curvature length during inflation lies just five orders of magnitude above the Planck length, making the transition from quantum geometry to effective fields our best probe of quantum gravitational physics. Our predictions for the gravitational effective theory of inflation are reported here:
Precision predictions of Starobinsky inflation with self-consistent Weyl-squared corrections
Eugenio Bianchi and Mauricio Gamonal
2506.10081 [gr-qc] (2025)
As we enter an era of precision cosmology, upcoming observations are expected to tighten constraints on many primordial observables, and precise theoretical predictions will be essential for next-generation GW and CMB surveys. You can find the methods for N3LO calculations of inflationary power spectra here:
Primordial power spectrum at N3LO in effective theories of inflation
Eugenio Bianchi and Mauricio Gamonal
2405.03157 [gr-qc] Phys.Rev.D (2024)
The quasi-de Sitter phase of inflation leads to a negative phase shift in pre-inflationary features:
Squeezed vacua and primordial features in effective theories of inflation at N2LO
Eugenio Bianchi and Mauricio Gamonal
2410.11812 [gr-qc] Phys.Rev.D (2025)
Parity-violating gravitational corrections are constrained by spinfoam γ-duality:
Spinfoams, γ-duality and parity violation in primordial gravitational waves
Eugenio Bianchi and Monica Rincon-Ramirez
2403.06053 [gr-qc] (2024)
Black Hole Information
Over long time scales, black holes are unstable because of the emission of Hawking radiation. Quantum gravity effects become dominant at late times. Quantum information methods, and in particular the Page curve and the relation between entanglement entropy and the energy-flux of Hawking radiation, provide a powerful tool for estimating these time scales:
Entanglement entropy production in gravitational collapse
Eugenio Bianchi, Tommaso De Lorenzo, Matteo Smerlak
1409.0144 [hep-th] JHEP (2015)White Holes as Remnants: A Surprising Scenario for the End of a Black Hole
Eugenio Bianchi, Marios Christodoulou, Fabio D'Ambrosio, Hal Haggard, Carlo Rovelli
1802.04264 [gr-qc] Class.Quant.Grav. (2018)
Entanglement in Energy Eigenstates
Two tools which can be found in every theorist's toolbox are the harmonic oscillator and random matrices. The Hamiltonian of most physical systems falls somewhere in between these two extreme idealizations. As a result, ensembles of Gaussian states and of random states provide a powerful tool for characterizing the typical behavior of the entanglement entropy in energy eigenstates of physical Hamiltonians, respectively in the integrable and in the quantum chaotic case. Here is a comprehensive report:
Volume-Law Entanglement Entropy of Typical Pure Quantum States
Eugenio Bianchi, Lucas Hackl, Mario Kieburg, Marcos Rigol, Lev Vidmar
2112.06959 [quant-ph] PRX Quantum (2022)
Together with M. Rigol, L. Vidmar, M. Kieburg and L. Hackl, we have used these methods to investigate entanglement in energy eigenstates of:
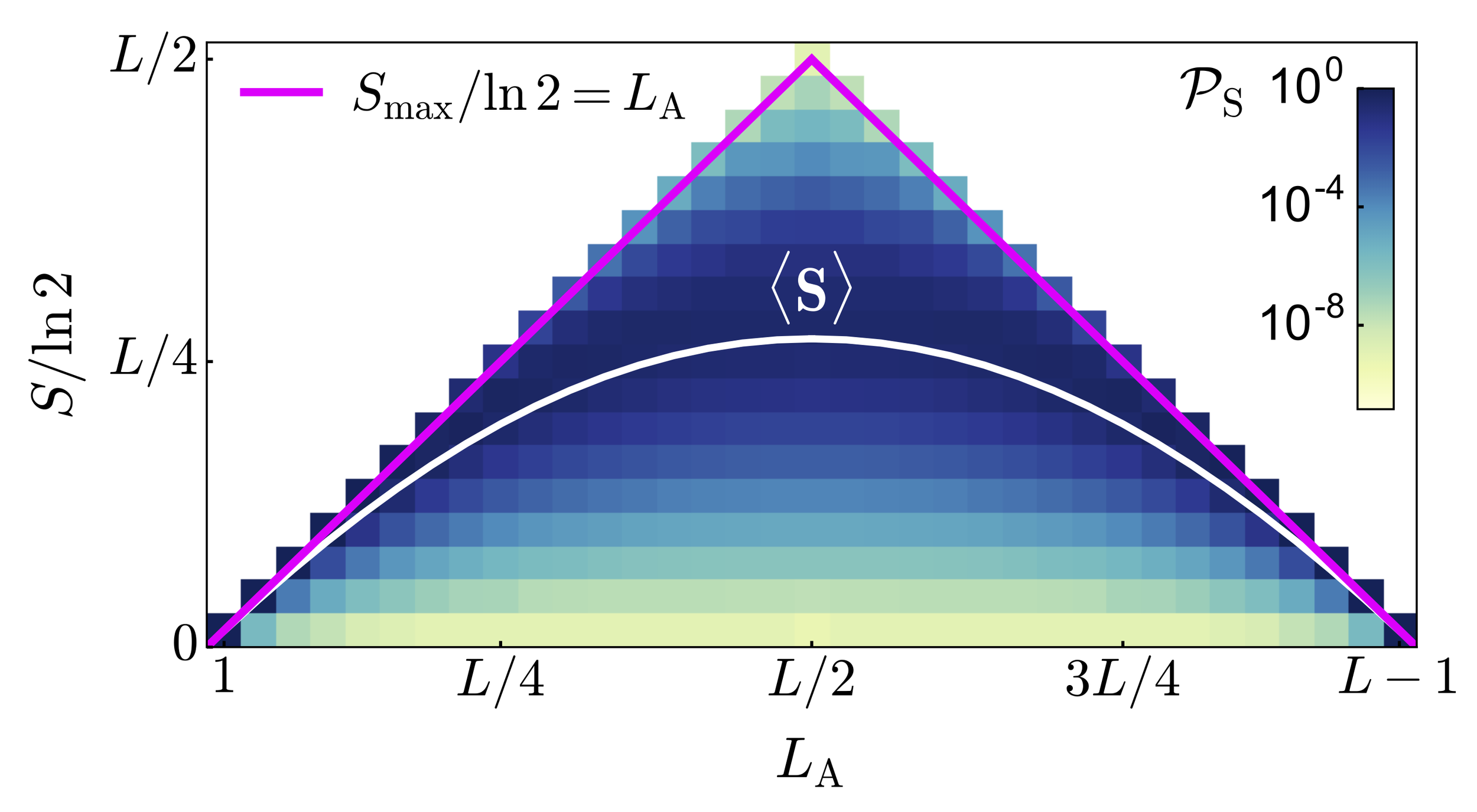
Entanglement in Random States
When a random pure state is restricted to a subsystem, its density matrix is practically indistinguishable from an infinite-temperature mixed state. If a constraint is introduced, such as a fixed total energy, the restricted state becomes close to a mixed state of finite temperature instead. The Page curve with constraints and its connection to thermodynamics is discussed here:
Typical entanglement entropy in the presence of a center: Page curve and its variance
Eugenio Bianchi and Pietro Dona
1904.08370 [hep-th] Phys. Rev. D (2019)
These methods extend to systems with non-abelian constraints, where the interplay of locality, symmetries, and entanglement, results in new phenomena:
Non-abelian symmetry-resolved entanglement entropy
Eugenio Bianchi, Pietro Dona, Rishabh Kumar
2405.00597 [quant-ph] SciPost Phys. (2024)
Entanglement in Gaussian States
Gaussian states have a rich geometric structure. In the Bosonic case, the canonical commutator defines a symplectic structure and the Gaussian correlation function defines a metric structure. In the Fermionic case these two structures are exchanged. In either case, there is a third structure built from the first two, the complex structure, which provides a powerful tool in computations of information-theoretic quantities. These methods are discussed in the comprehensive report:
Bosonic and Fermionic Gaussian States from Kähler Structures
Lucas Hackl and Eugenio Bianchi
2010.15518 [quant-ph] SciPost Phys.Core (2021)
We have applied these methods to:
Bosonic Lattices with N. Yokomizo and L. Hackl (PRD 2015)
Fermionic Gaussian States with M. Rigol, L. Vidmar, M. Kieburg, L. Hackl (PRL 2017, PRL 2018, PRB 2019, PRB 2021)
Loop Quantum Gravity with L. Hackl, J. Guglielmon and N. Yokomizo (PRD 2016)
Quantum fields and the Area Law with A. Satz (PRD 2019)
Adiabatic Vacua in Cosmology with L. Hackl and Y. Ghelem (2025)
Quantum Chaos and Thermalization
For a large class of many-body systems it has been observed that, in a quantum quench, the entanglement entropy of a subsystem A evolves in time going through three phases: (i) an initial transient which depends on the details of the initial state, (ii) a phase of linear growth where the entanglement entropy grows with slope ΛA, and (iii) a saturation phase where the entropy approaches an equilibrium value and fluctuates statistically around it. In the paper:
Linear growth of the entanglement entropy and the Kolmogorov-Sinai rate
Eugenio Bianchi, Lucas Hackl and Nelson Yokomizo
1709.00427 [hep-th] JHEP (2018)
we prove a theorem that shows that for semiclassical bosonic systems the linear phase (ii) has slope ΛA given by the sum of the positive Lyapunov exponents of the associated classical system restricted to A. This phenomenon appears to be robust and has been conjectured to apply to a larger class of quantum chaotic systems and systems with bosonic instabilities, including quantum many-body systems and quantum fields in curved spacetimes, where instabilities give rise to a wealth of non-equilibrium phenomena.
Lecture Notes on General Relativity
Notes of my lectures on General Relativity for graduate students at Penn State (PHYS 510 and PHYS 511):
-GR1-
GR1-Lec00 - Introduction and Syllabus
GR1-Lec01 - Manifolds
GR1-Lec02 - Tensors
GR1-Lec03 - Covariant Derivative
GR1-Lec04 - Geodesic Deviation
GR1-Lec05 - Intrinsic Geometry of Surfaces
GR1-Lec06 - Diff. Geom. Discussion HW1
GR1-Lec07 - Spacetime Geometry
GR1-Lec08 - Particles and Local Frames
GR1-Lec09 - Redshift
GR1-Lec10 - Energy-Momentum Tensor
GR1-Lec11 - Symmetries Killing Vectors and Conservation
GR1-Lec12 - Action EoM and Matter
GR1-Lec13 - Einstein Eqs and the Action Principle
GR1-Lec14 - Tidal Forces and Curvature
GR1-Lec15 - Schwarzschild Black Hole and t-r coord
GR1-Lec16 - Schwarzschild Black Hole and v-r coord
GR1-Lec18 - Gravitational Redshift
GR1-Lec19 - Model of a Relativistic Star and TOV Eq
GR1-Lec20 - TOV and Neutron Star
GR1-Lec21 - Gravitational Waves and Perturbation Theory
GR1-Lec22 - Gravitational Wave Sources
GR1-Lec23 - Gravitational Wave Power
GR1-Lec24 - Black Holes Discussion HW4
GR1-Lec25 - Cosmology Homogeneity and Isotropy
GR1-Lec26 - Cosmology Friedmann Eq
GR1-Lec27 - Cosmological Redshift
GR1-Lec28 - Cosmological Parameters
GR1-Lec30 - The meaning of Einstein Equations
-GR2-
GR2-Lec00 - Introduction and Syllabus
GR2-Lec01 - Intrinsic and Extrinsic Curvature
GR2-Lec02 - Foliations ADM Variables and ADM Action
GR2-Lec03 - Action for Gravity
GR2-Lec04 - Hamiltonian GR
GR2-Lec05 - Hamiltonian Constraint
GR2-Lec06 - Boundary Terms and ADM Energy
GR2-Lec07 - Vaidya model of collapse
GR2-Lec08 - TOV Equation and Neutron Stars
GR2-Lec09 - Spherical Symmetry and Reduced Action
GR2-Lec10 - Black Hole Perturbations and Quasi Normal Modes
GR2-Lec11 - Redshift, Raytracing, and Hawking Radiation
GR2-Lec12 - Black Hole Horizons
GR2-Lec13 - Inflation and the CMB
GR2-Lec14 - Inflationary Background and Slow-Roll
GR2-Lec15 - Perturbations of FLRW and the SVT Decomposition
GR2-Lec16 - Action for Scalar, Vector, and Tensor Perturbations
GR2-Lec17 - Mode Functions and Quantum Perturbations
GR2-Lec18 - Bunch-Davies Vacuum and Power Spectrum
GR2-Lec19 - Gaussian Random Fields and Power Spectrum
GR2-Lec20 - Adiabatic Vacua and WKB methods
GR2-Lec21 - Green-Function Method and Power Spectrum at NLO
GR2-Lec22 - Inflation, N-efolds, and Power-Spectrum
GR2-Lec23 - Initial State and the Power Spectrum
GR2-Lec24 - R+R2+W2 Inflation
Homework Assignments:
GR1-HW1 - Differential Geometry
GR1-HW2 - Spacetime and Matter
GR1-HW3 - Einstein Equations
GR1-HW4 - Black Holes
GR1-HW5 - Gravitational Waves
GR1-HW6 - Cosmology
GR2-HW1 - Hamiltonian Formulation
GR2-HW2 - Black Hole Perturbations
GR2-HW3 - Cosmological Perturbations
Lecture Notes on Loop Quantum Gravity
Notes of my lectures on Loop Quantum Gravity for graduate students at Penn State (PHYS 565):
QG-Lec00 - Introduction and Syllabus
QG-Lec01 - Quantum Plane and Area Spectrum
QG-Lec02 - Quantum Tetrahedron and Volume Spectrum
QG-Lec03 - SU2 Intertwiners and Penrose Spin-Geometry
QG-Lec04 - Quantum Polyhedron and Coherent States
QG-Lec05 - Spin-Networks and Diagrammatics
QG-Lec06 - Spin-Networks and Graph Hilbert Space
QG-Lec07 - Regge Calculus and Curvature
QG-Lec08 - Twisted Geometries and Phase Space
QG-Lec09 - Yang-Mills and Holonomy-Flux
QG-Lec10 - Einstein-Cartan Action and Barbero-Immirzi Parameter
QG-Lec10b - Additional Material on Frame Fields and Exterior Derivatives
QG-Lec11 - GR in Ashtekar Variables
QG-Lec12 - Holonomy-Flux Algebra
QG-Lec13 - Topological Field Theory
QG-Lec14 - BF Phase Space
QG-Lec15 - Topological Field Theory with Defects
QG-Lec16 - TQFT with Defects and LQG
QG-Lec17 - Covariant Path Integral
QG-Lec18 - Gravity 2+1 and Ponzano-Regge
QG-Lec19 - EPRL Spinfoam Vertex
QG-Lec20 - EPRL and gamma-simple irreps
QG-Lec21 - EPRL and Ponzano-Regge asymptotics
QG-Lec22 - Area law and semiclassicality
Lecture Notes on Mechanics & Orders of Magnitude
Notes of my lectures on “Mechanics & Orders of Magnitude” for Honors students at Penn State (PHYS 211H):
Mech-Lec01 - Syllabus and Order of Magnitude Estimates
Mech-Lec02 - Velocity and Acceleration
Mech-Lec03 - The Three Laws of Mechanics
Mech-Lec04 - Air Drag and Free Fall
Mech-Lec05 - Energy, Work and Power
Mech-Lec06 - The Harmonic Oscillator
Mech-Lec07 - Vectors and the Laws of Mechanics
Mech-Lec08 - Momentum, Impulse and Collisions
Mech-Lec09 - Review Theory
Mech-Lec10 - Review Estimates
Mech-Lec11 - Circular Motion
Mech-Lec12 - Angular Momentum
Mech-Lec13 - Rigid Bodies
Mech-Lec14 - Rotational Energy
Mech-Lec15 - The Pendulum
Mech-Lec16 - Gravity and Orbits
Homework Assignments:
HW01 - Calculus and Orders of Magnitude
HW02 - Air Drag and Free Fall
HW03 - Energy, Work and Power
HW04 - Momentum, Impulse and Collisions
HW05 - Angular Momentum and Torque
HW06 - Oscillations and the Pendulum
Updates:
- September 2025 -
The next Loop Quantum Gravity School will be held at Les Houches in Sept. 2025. You can find the program here:
